What is DARTS? An Overview
It is a math intervention model that uses instant data collection of weekly diagnostics to assign individualized intervention for students as well as frequent formative data for teachers to target instruction. Translations and Story Problems build students' math vocabulary, conceptual understanding, and challenge them to higher order thinking. The use of a common graphic organizer and common rubric school-wide builds lateral and vertical consistency throughout a school's math department and strengthens math instruction. DARTS (Diagnostic, Assessment, Rescue, Translations, Story Problems) is a home-grown in-house intervention model that can be duplicated in any school, any size. It has been effective for students in grades 5-12, but has mostly been utilized in grades 6-8. It is designed to find the "holes" in math skills and knowledge that students come in with, fix them strategically, and provide students with high level access to the grade-level curriculum at the same time. I like to use the analogy of thinking of students as a cup. They come in with holes, and we try to pour in new information that seeps out of the holes, because they lack some of the foundational skills. DARTS works to plug those holes so that new information stays and students can do the grade-level math.
Diagnostic
The diagnostic is a 10-question multiple-choice (a-d) quiz given once every week in the math class. The same diagnostic is given for the entire grade/math level from SDC to Gifted. For lower grade levels, it typically takes no more than 20 minutes for students to finish the 10 questions. They may take longer on harder Algebra problems. The diagnostic should be given "cold" at the beginning of the period to gather what students genuinely know. Students should show all work, and the diagnostic should be given in a CST-like environment (monitored by teacher, no noise, no assistance, etc.).
Creation of the Diagnostic
The first diagnostic begins with some key basic skills that students should have mastered before entering their current grade level. Use the question: "What do I want students to have mastered before coming to my class that will ensure their success this year?" Questions should be as basic and skill-based as possible to begin. Distractor/wrong answer choices must be carefully chosen to target specific student errors, common misconceptions, and common student mistakes. The goal is to be able to infer what mistakes students are making when they chose a particular wrong answer. When a large number of students choose one of the wrong answers, it is easier to point out and correct their mistake rather than reteach an entire concept. Students can also be asked to do error analysis on the wrong answer choices as a differentiation strategy.
With the exception of the first diagnostic given every year, each diagnostic is newly developed based on the previous week's school-wide data. Each question has a benchmark goal: 70% (this number can vary). If the school-wide data from a question reaches the benchmark, then that question can be considered "mastered" and is removed from the diagnostic. Another question in the progression of the learning of mathematics should replace it. However, if a question does not reach the goal, then that question will repeat on the following week's diagnostic (numbers should be changed). A question remains on the diagnostic until it reaches the benchmark. For example, a question might be -9+5=, and the answer choices are strategic to target common student errors in this type of problem. Even if the percent of students getting it correct begins at 25%, that type of problem will stay on the diagnostic until it reaches 70%, and each week we are looking for growth. So the following week, that same question might become -7+4=.
Diagnostics are created using ExamView software and question banks gathered from textbook publishing companies. However, if a particular kind of question is not available, then one can be hand-created. All questions and answer choices from the question banks can also be modified. With the addition of each question always use the following questions: "What can I learn from this problem by the wrong answers that students choose?" and "Have I tested enough pre-requisite skills for students to be able to do this problem? Is this basic enough?" One trap that those making diagnostics succumb to is jumping into too difficult of a problem without testing the prerequisites first. For example, a question like 4-|5-7|= is testing too much: absolute value, subtraction of integers, and order of operations. Previous questions on the diagnostic that address all of these more basic skills must be tested before using a question like this.
FAQ About the Diagnostic
Who creates the diagnostic? Someone who has deep knowledge and expertise of the math content standards and the progression.
What if one teacher or a few classes have not met the benchmark but it was made as a school? Does the question still come off? You cannot let individual classes hold back the whole grade level. Those classes may be progressing slower than the rest or that teacher may need more instructional support. The creation of the diagnostic is for the betterment of the whole grade level - let the rescue assignment be the individual intervention for students.
Data Collection & Analysis
Teachers must collect and input the number of students who chose a, b, c, and d on each question and record it on the Google Spreadsheet. The spreadsheet takes those numbers to calculate the total responding, percent correct, average percent correct, best distractor, and develop graphs.
Suggested methods of data collection include 4-corners and GradeCam. For the 4-corners method, label the 4 corners of the classroom with A, B, C, and D. Have students use a diagnostic other than their own (to avoid embarrassment if a student ends up in a corner by him/herself). The teacher calls out the question number, and the students go stand in the corner that matches what is on the diagnostic for that question. For example, the teacher calls question #1, and the paper Joe is holding has C chosen for #1, then he will go stand in the corner marked with C. After all students have gone to the respective corners, the teacher takes a count of the number of students in each corner and records them before moving to the next question. Unanswered questions should be omitted from the data.
Teachers should project the data for the students to see and analyze. There are data from the entire grade level, teacher level, and individual class level. Data are reviewed to see which questions the class did the worst on (for whole-class review) and specific distractors that many students chose to purposefully correct common mistakes.
Assessment
The DARTS model emphasizes the need for benchmark core-content assessments. The purpose of the diagnostic is intervention; it is NOT to test standards that were just taught. The DARTS model is in addition to (a layer on top of) the core math content. Therefore, it is beneficial to also have bi-monthly or quarterly benchmark assessments that do check the core content standards for the grade level. These assessments should be taken seriously, implemented rigorously, and data analyzed vigorously. Data from these assessments should be disaggregated by subgroups, monitored by administration, compared to previous years, and used to inform review and instruction moving forward.
Rescue Assignment
The rescue assignment is designed to match each week's diagnostic. It is differentiated intervention for students based on what each student needs to practice, providing instant feedback for what the student needs to master. For each of the ten questions on the diagnostic, there are 3-4 free-response questions on the rescue. Each student does the corresponding problems for each problem that s/he missed on the diagnostic. Some teachers will also assign problems on the rescue for which the student did not show enough work for on the diagnostic. Students are NOT to do the entire rescue assignment as "extra practice." That is not the design of the model. For example, if a student missed #2, 3, and 8 on that week's diagnostic, s/he would do #2, 3, and 8 on the rescue assignment, which would be about 12 extra homework questions. It is also a motivational tool - if a student gets a 10 out of 10 on the diagnostic, then s/he has no extra work to do, so it pays off to put in effort on the diagnostic.
Creation of the Rescue
To create the rescue assignment, first build the diagnostic. You do not need the data from the diagnostic in order to make the rescue. They can be done simultaneously. Say, for example, the first diagnostic question is "Simplify 8/24 to lowest terms." Some common mistakes and misconceptions that students make will be in your answer choices along with the right answer of course. On your rescue for the first question, you might put "1. Simplify each fraction to lowest terms." Then you'll have four parts with fractions that could be simplified: e.g. 1. 4/12 2. 9/18 3. 12/30 4. 4/20. See the rescue assignment example in the DARTS handouts to see the set-up. Traditionally, Microsoft Word is used to create the rescue assignment. It helps streamline formatting, and there is an excellent equation editor that can show all math symbols and spacing properly.
FAQ About the Rescue
Is it homework or classwork? It can be either. Some teachers go over a few questions that the whole class needs to work on. If students are not good about turning in homework, then it is recommended to give them some class time to work on their rescue assignment. Doing the rescue is a great way to put students into purposeful groups, have tutorials, or differentiate instruction.
How do you grade the rescue? Most teachers have students staple their rescue assignment to their diagnostic, so it is easy to see that they did the questions they needed to. Grade it like you would grade any other classwork or homework assignment. Teachers also use the rescue as an opportunity for students to make up points that they missed on the diagnostic.
If a student misses a problem because he doesn't know how to do it, why assign four more problems that he doesn't know how to do? For some problems you will do a mini-lesson or reteach if the majority of the class did not do well. Other problems will be missed by only a few students. It is our job as teachers to empower students to be their own advocates. We must teach them how to learn something once they know they don't know how to do it. What are their resources? How about asking a friend, ask a teacher, stay for tutoring, AVID tutorials, look in the book, look back in their notes, search online, utilize Kahn Academy or Youtube, ask a parent or older sibling? There are many ways students can find information if we point them in the right direction. There are even some teachers who will solve each question from the diagnostic in class or post solutions worked out on their website.
Translations
Translations are math phrases completely written out in English words, which students translate into math symbols. In the younger grades an example would be five plus six, to which we would want the student to write 5+6. Other examples could be: the sum of a number and nine, twice the difference of two numbers, the perimeter of a square, or twenty nickels and dimes totals one dollar and sixty cents. Students do not solve translations.
Teachers introduce 10 new translations per week, however they decide to divide them up (two in a warm-up each day, split in half over two days, or all at once). The translations are pre-developed and in sets that follow the progression of the grade level and build from literal translations to more abstract and conceptual understanding.
Translations are not just exercises - they are opportunities to engage in rich mathematical discussions utilizing proper vocabulary. A discussion about the ways to translate half a number engages students and can lead to a much deeper understanding. Possible answers should be shared and discussed, and teachable-moments should be utilized. The class should come to a consensus about which symbolic representation is "best" or "the most correct." Correct mathematical vocabulary must be used by both the teacher and the students at all times.
Full-year sets of translations have been developed for grades 6, 7, Algebra Readiness, and Algebra 1.
Story Problems
A story problem is a word problem. The DARTS model requires students to engage with at least one story problem per week. This requirement can be met by doing one individually or in groups. Every story problem must follow the common (school-wide) graphic organizer and rubric.
The story problem is meant to build conceptual understanding of the core content. Use easy problems to get students used to using the graphic organizer and rubric, then go on to more challenging problems. Problems chosen should fit into the core curriculum, but can be differentiated to meet the various needs of students.
Every classroom implementing DARTS must have evidence of story problems posted in the room. They should reflect the use of the graphic organizer and be graded by the rubric.
Common Graphic Organizer
Every story problem must be completed using the common graphic organizer. This graphic organizer is based on the theory of using multiple representations to build mathematical understanding (like the 4-fold method). Once students get used to filling in the graphic organizer, tackling word problems becomes much easier. Since it is used school-wide, once the lowest grade level learns how to do it, subsequent grade levels do not need to re-teach the process.
Common Rubric
Every story problem must be graded using the common rubric. This rubric is based on the theory of feedback and knowledge of expectations/results. Students should have practice grading each other's work to familiarize themselves with the rubric requirements.
DARTS at Edison Middle School - What the Data Show
DARTS began at Thomas A. Edison Middle School (EMS) of the Los Angeles Unified School District (LAUSD) in 2009. This 3-track, year-round school served nearly 1,900 students in 6th, 7th, and 8th grade. Located in the heart of South-Central Los Angeles, EMS serves 100% neighborhood kids - there is no magnet program.
| Socioeconomically Disadvantaged | 99% |
| Latino | 97% |
| African American | 3% |
| English Learners | 40% |
| Students with Disabilities | 11% |
| Student Enrollment | 1891 |
| Socioeconomically Disadvantaged | 93% |
| Latino | 98% |
| African American | 2% |
| English Learners | 25% |
| Students with Disabilities | 11% |
| Student Enrollment | 1193 |
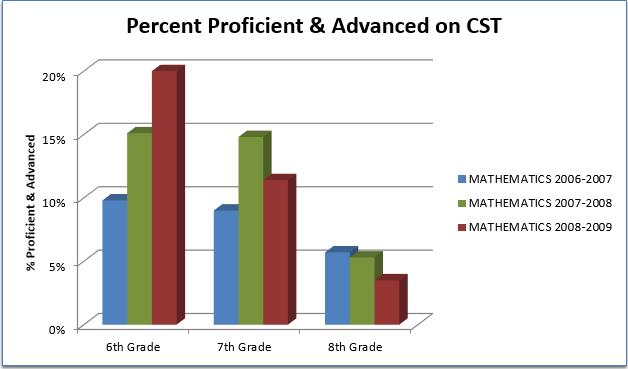
Edison math data before beginning DARTS
In the 2009-2010 school year, EMS was on a 7-period day, each academic period lasting about 53 minutes (and 38 minutes on Tuesdays to make room for Professional Development). There were no math intervention classes. All math teachers in all grades and all tracks (including SDC and gifted) were required to implement all components of DARTS.
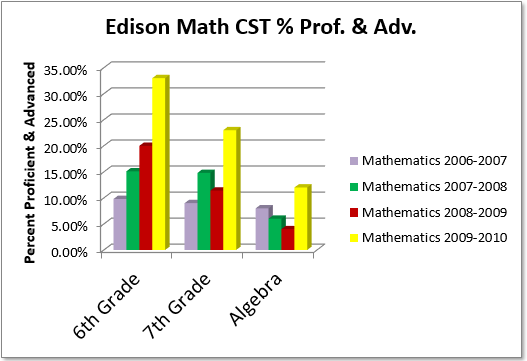
Edison math data after 1 year of DARTS
After implementing the model for one year, the CST data showed significant growth in mathematics. In the percentage of students scoring proficient or advanced in math, 6th grade increased 13%, 7th grade increased 12%, and Algebra increased 8%, for a net gain of 33%. That same year, English had a net gain of 1%, Science gained 4%, and History had no change.
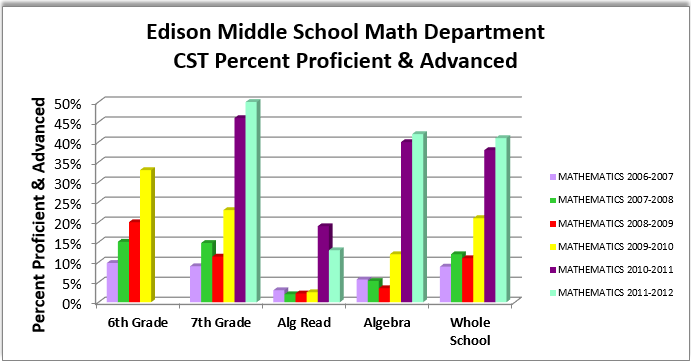
Edison MS Math Data
In the 2010-2011 school year, EMS went off of year-round and became traditional. One third of the students had to leave, and the district decided to have those third be the entire 6th grade. EMS became a 7th and 8th grade middle school. The school also switched to an 8 by 2 block schedule where every student gets a period of math and another period of math-support with the same teacher (double block) in order to support the DARTS model implementation. At the end of this second year of implementation, Edison Middle School had the largest 1-year gain in mathematics of any school in the entire LAUSD. After only two years, EMS went from having 4% of Algebra students proficient or advanced to 40%.
Students who come into EMS having 6th grade in elementary school have math scores that are (on average) about 8-10% lower than 6th graders in middle school. The 7th graders of 2011-2012 overcame that, and 50% of them scored proficient or advanced on the CST. In 2011-2012, EMS made their 8th grade Algebra program stronger by having 70% of 8th grade general ed students in Algebra, and only 30% in Algebra Readiness (a curriculum for students who are not deemed ready for Algebra). Typically, when more students are put into Algebra, scores drop, but EMS still managed to gain another 2%. Algebra Readiness students did have a drop in scores that year, but that is attributed to making sure only the students who are greatly struggling with math take that course, and having any students jump multiple band levels in one year is astounding.
In February 2012, the Miramonte Elementary School scandal hit the community of EMS. Being EMS's biggest feeder school, the uprooting of all staff at Miramonte had a great impact on the students that would/will become EMS's students. The faculty and staff at EMS look forward to creating new relationships with Miramonte and all of its feeder schools in order to create a better articulation method laced with common strategies and programs to enhance student success.
DARTS and the Common Core State Standards
The question often comes up: "How do you see DARTS changing with the implementation of the Common Core?" There is no doubt that the Common Core State Standards (CCSS) will change the DARTS model and all of mathematics instruction. Teachers who have been implementing DARTS for several years now have had conversations and ideas as to how this might look and what the vision for DARTS will be in relation to academic success in math under the CCSS.
Translations and Story Problems will become the central focus of the DARTS model. When taught properly, translations fit in perfectly with Mathematical Practice (MP) #3: Construct viable arguments and critique the reasoning of others, MP #7: Look for and make use of structure, and MP #2: Reason abstractly and quantitatively. We have thrown around the idea of having the students do reverse-translations, which would involve giving students symbolically written math expressions and asking them to write them out in English phrases. In our review of the Smarter Balanced assessments, students will have to explain their answers in text boxes. Being able to explain the math without symbols will be vitally important. How else can a student say that he used the formula A=πr2 with only the standard keyboard?
Story problems are central to the transition to CCSS. MP #1: Make sense of problems and persevere in solving them. We must give students opportunities to do this on a regular basis. The incorporation of a really good story problem will have students using all of the MPs in order to arrive at their answer and explain the process. By using the graphic organizer and rubric, we can better guide students to incorporate more of these higher level thinking requirements. The use of story problems in the DARTS model will not change. What may change are the story problems that we choose and the level of expectation of their answers. It has also been suggested that the use of a group performance task be practiced once or twice per month in lieu of the weekly story problem to get students prepared for the Smarter Balanced assessment.
The most controversial topic in the overlap of DARTS and CCSS is the diagnostic and rescue assignment. Popular thought is that if students will no longer be assessed using multiple choice tests, then the diagnostic should change or be eliminated. However, that is not the vision. Recall that the purpose of the diagnostic is intervention - to pinpoint skills and comprehension weaknesses that students have, make educated guesses about their common misconceptions and mistakes, and correct those strategically. If multiple choice diagnostics are eliminated, there is no way to collect this information. This information is crucial. Of course, new types of questions may be introduced to prepare students for the select response types. Questions that have choices like I and II, I and III, only II, I, II, and III to help students go through multiple answer options may help them prepare for the new assessment while also giving us information about their needs.
The data from a diagnostic and the rescue assignment provide students with immediate individualized feedback, which is proven by research to help students improve. The elimination of the diagnostic will not help us in the intervention process. Teachers will not need to spend time on test-taking techniques or strategies, and students may be asked to show their work without utilizing answer choices.
Whatever changes come about, DARTS is a "home-grown" model that is able to adapt. If you have ideas to better the model, you are welcome to contact Heather Karuza. With our collective minds, we can make sure that the DARTS model helps close the achievement gap and puts all students on a path of mathematics achievement.




